|
| |




Next: 2.2 Derivative Dispositions
Up: 2. Dispositions
Previous: 2. Dispositions
Subsections
Nearly everything we do from day to day is influenced by dispositions
and knowledge of dispositions. The concept of `dispositions' is central to
this whole book, and as I will be arguing that they are the neglected and
misunderstood key to any realistic understanding of nature, I will take
some time to explain their meaning.
To say that salt is soluble in water, that this piece of metal is
flexible, that glass is fragile, or that steel is hard, is to ascribe
dispositional properties to these things. These are the kinds
of things that can be determined by experimental investigations, and are
general facts for which we can collect evidence. Often a single trial will
be sufficient to determine, say, that salt does dissolve in water when
suitably immersed. The meaning of saying that salt is soluble, we should
note, goes beyond reporting the results of our few experiments. It is to
say that it is a general property of salt that whenever it is
placed in water, then it will dissolve. Similarly, to say that
this piece of metal is flexible, is to say that whenever it is
subject to a transverse pressure, then it will bend. To say
that steel is hard is to say that whenever it is subject to a force, then
it will be only slightly deformed. To say that glass is fragile is to say
that whenever it is suitably hit it will break.
What is important about dispositional properties is this `if 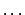 then then 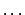 ' feature. Dispositions are thus different from other
properties such as place, size and shape which describe only present
states of affairs, and make no reference to what might happen in the
future. For this and other reasons, there has been considerable debate
within the philosophy of science as to the extent and importance of
dispositional properties, against what we might call purely static or
structural properties. ' feature. Dispositions are thus different from other
properties such as place, size and shape which describe only present
states of affairs, and make no reference to what might happen in the
future. For this and other reasons, there has been considerable debate
within the philosophy of science as to the extent and importance of
dispositional properties, against what we might call purely static or
structural properties.
The issue of dispositional versus static properties will be
considered latter in the chapter, for it is important, as Mackie [1973]
points out, to separate three different sorts of question: questions
about meaning, about what is being said when dispositions are
ascribed to things; questions about what we know, about when
and how we are able to ascribe dispositions to things; and
questions about what is there, about what sorts of properties
or states or processes are objectively present in the things that we
describe in dispositional terms. To these, I add questions of
reality, whether we can completely avoid dispositional terms, and
questions of explanation, as to how dispositional properties
are in fact explained scientifically.
A great many terms have been used over the years to describe what we call
here `dispositions' or `dispositional properties'. In a very general
sense, any `ability', `capability' or `capacity' refers to a
meaning of this sort, but as these words have meanings far beyond the
philosophy of nature, we will not adopt them as technical terms.
Aristotle used the term dynamis (potentiality) to refer to the
general capability of things to cause changes in others. Locke [1706] used
the term `power', and says that fire has a power to melt gold,
and gold has a power to be melted; that the sun has a power to blanch wax,
and wax a power to be blanched by the sun. We are abundantly furnished
with the idea of `passive power', he points out, by almost all sorts of
sensible things. More recently, Harré2.1
has revived the word `power' as a general term for scientific
explanations, and his powers are either identical with dispositions or
closely related to them.
In science, terms such as `force' and `potential' (as in `potential
energy' or `field potential') have been introduced, and these are all
dispositional in an essential manner.
I will be using the terms `power', `potential',
`capability', `capacity', `propensity' and `cause'
all as examples within the class or category of `dispositional
properties of objects'. (There will be more discussion of these
different terms in chapter
7.)
Propensities: Probabilistic Dispositions
Not all dispositions are what Mackie [1973] calls `sure-fire'
dispositions. Those are the dispositions, like the solubility of salt and
the hardness of steel, which are always manifested if the disposition is
still in fact present. Other dispositions may manifest themselves only
probabilistically. The disposition of a radioactive nucleus to decay, for
example, does not manifest itself as a definite event immediately after
the nucleus was formed: that is just when the decay first becomes
possible. Instead, the disposition to decay appears as a
certain propability to decay in any time interval. And
furthermore, this propability may vary with time even while
(i.e. before) it is not being manifested.
After Popper [1959], we use the term propensity to refer to
dispositions with any kind of probabilistic outcome. They will clearly
come in handy when we want to describe quantum mechanics.
Propensities are properties of objects which, in appropriate
circumstances, give rise to real and objective
probabilities. These probabilities, if they are truly the product of
propensities, are not merely an expression of ignorance or partial
knowledge on our part.
We sometimes still consider dice to have propensities for landing with
different numbers upward. As this is only because of our ignorance of
their exact trajectories, however, they only have `propensities' in a
secondary or `subjective' sense2.2.
Exactly whether and how there can be any real
and objective propensities will be discussed below, in the context of that
question for dispositions in general.
Kyberg [1974] and Maxwell [1976] have more specific discussions of the
probabilistic aspects, and give detailed comparisons with the frequency
interpretation of probabilities.
Humphreys [1985] discusses the question of whether talk of propensities
can be replaced by talk of probabilities.
Questions of Meaning
If we want to know what it means when we say that salt is
soluble, we will need to know that the `if 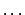 then then 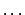 '
phrase means. We need to specify both the antecedent condition, the
manifesting occurrence, and the logic of the `if '
phrase means. We need to specify both the antecedent condition, the
manifesting occurrence, and the logic of the `if 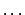 then then
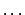 ' expression.
In general, the ascription of properties in
dispositional category is of the form ' expression.
In general, the ascription of properties in
dispositional category is of the form
Object S has the disposition P to do action A
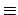 if S is in some circumstance C, C depending on P and
the character of A,
then there will be a non-zero likelihood of S doing A. if S is in some circumstance C, C depending on P and
the character of A,
then there will be a non-zero likelihood of S doing A.
Here, the `action A' can either be a change in S itself or an
interaction with other objects. The suitable `circumstance C' is
usually defined by multiple spatial relations to other objects, and will
be different for different dispositions for different actions. The
circumstance C is said to depend only on the `character' of the
action, and not the action itself, because possibly, if the disposition is
never manifested, there may exist no such action, at any time
in the past, present or future. The circumstance C should depend only
of the kind of event expected, and not on its actual
occurrence. Finally, the phrase `non-zero likelihood' is designed to be
sufficiently general to allow both sure-fire dispositions and
probabilistic propensities. It has the consequence that if the probability
of an event (while varying with time) touches zero, then there is no
propensity at that particular time, but this is surely a reasonable
feature.
Harré and Madden [1975] add a phrase `in virtue of the constitution
of S' to the above form, in order to exclude `changes' to certain
properties of S that are changes in purely external relations that may
come about completely independently of whatever S is actually like. Thus,
for example, no disposition of Socrates is necessary to explain his
becoming smaller than Theaetetus, if it is the latter who is growing.
Mackie [1973] argues however, that it is not part of the logical
meaning of a disposition that it is based on some internal form of
the objects concerned. He admits that the existence of some basis is an
extremely plausible empirical hypothesis, but not that it is logically
implied by every ascription of a disposition on all occasions. This
question of `basis' will be further discussed below.
As is well known, the logical meaning of the `if 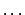 then then
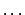 ' expression italicised in the above form of ascription can not
be taken to simply be the material conditional. The meaning of `x is
fragile' -- F(x) -- cannot be defined as ' expression italicised in the above form of ascription can not
be taken to simply be the material conditional. The meaning of `x is
fragile' -- F(x) -- cannot be defined as
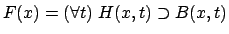 |
|
|
(2.1) |
where H(x,t) means `x is hit at time t' and
B(x,t) means `x breaks at time t', because this would
make fragile every object that was never hit. If we defined
F(x,t) to mean x is fragile at time t', then
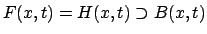 |
|
|
(2.2) |
would make fragile at t every object that was not hit at time t.
Mackie [1973] describes a variety of alternative logical expressions
designed to capture the required if/then meaning, and how their
inadequacies indicate that we need conditionals which are not themselves
purely material conditionals.
Neither, he and Mellor point out, can dispositional statements involve
purely counterfactual conditionals, as then we get the absurd
result that salt is no longer soluble once it is dissolved.
D'Espagnat [1979] explains how one could try to use what Carnap called
`partial definitions' for the meaning of dispositional terms. This amounts
to translating the statement `x is fragile at time t' into a
`reduction sentence' of the type
If x is hit at time t, then it is called fragile if and only if it
breaks.
or, in the language of predicate calculus,
 |
|
|
(2.3) |
This definition can be verified not to suffer from the deficiences of the
previous proposals. On the other hand, d'Espagnat points out, the range of
definition (2.3) is obviously much smaller than that of definition
(2.2). This is because (2.3) yields no interpretation for a
statement such as `object x is fragile and it is not being hit'. If no
other partial definitions of `fragility' are then applicable, the
statement turns out, to the logician, to remain incomprehensible and even
meaningless.
The conclusion both Mackie and d'Espagnat come to is that dispositional
statements are equivalent to some kind of non-material conditional outside
the range of traditional (non-modal) formal logic. They cannot,
furthermore, be identified specifically with counterfactual conditionals.
The if  then in then in
F(x,t) = if H(x,t) then B(x,t)
is therefore non-material: whether the statement would take an open,
subjunctive or counterfactual form depends on the circumstances and on the
speaker's beliefs about the circumstances. If the glass was known not to
be hit at time t, then a counterfactual form is appropriate; if it was
known to be hit at time t, then we have simply F(x,t) 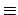 B(x,t); whereas if it is not known whether it was hit or not, then
we use the subjunctive form `if the glass were to be hit, then it would
break'. B(x,t); whereas if it is not known whether it was hit or not, then
we use the subjunctive form `if the glass were to be hit, then it would
break'.
These implications together amount to what Mackie calls a minimal
disposition. The ascription of a minimal disposition is taken as
equivalent to the assertion of a suitable non-material conditional, and
this encompasses a large part of the everyday meaning of dispositional
properties. They allow dispositions to be ascribed both when they are
being manifested and when they are not. They allow glass to be fragile for
a while, and then to be toughened by heat-treatment and to be fragile no
longer. They allow a piece of wrought iron to have a period of brittleness
when it was cooled to then temperature of liquid air. They also allow a
thing to have a disposition even if neither it or anything else ever
manifests that disposition
(such as the disposition for a nuclear explosion, to use an example from
Mellor [1974]).




Next: 2.2 Derivative Dispositions
Up: 2. Dispositions
Previous: 2. Dispositions
Prof Ian Thompson
2003-02-25
|
![]()