|
| |




Next: 12.3 Mind-dependent Actualisation -
Up: 12. Measurements and Other
Previous: 12.1 The Problem of
Subsections
12.2 Objective Actualisation - some proposals
The problem addressed in the remainder of this chapter is the
specification of the precise conditions for the actualisation
of propensities. Propensities have been construed to be propensities
for actualising events, but we have not yet said
when these events occur, or even under which conditions they
become more likely. In the terminology of chapter
2,
while the propensities may be the `principal cause' of the actualising, we
have still to determine the conditions or `instrumental causes' of their
operation. This is because dispositions in general have to have
appropriate conditions before they have a non-zero probability of
manifesting themselves. Indeed, the very ascription of dispositions made
this clear:
Object S has the disposition P to do action A
 if S is in some circumstance C, C depending on P and
the character of A,
then there will be a non-zero likelihood of S doing A. if S is in some circumstance C, C depending on P and
the character of A,
then there will be a non-zero likelihood of S doing A.
The suitable `circumstance C' was considered in chapter
2to be defined by multiple spatial relations to other objects, but this is
not a necessary definition: it could just as well be defined by
differences of energy, of numbers of interactions, of durations, or
of gravitational effects on the space-time metric, to name some of the
conditions that have been proposed. These options will be considered
in detail below. It will turn out to be rather implausible that
the conditions for the actualisation of the fundamental `propensities for
actual events' depends simply on spatial distances, though at one time
this was seriously considered.
12.2.1 Simple schemes
Faber [1986] provides a useful catalogue of what he calls `materialistic
hypotheses' for answering the question ``When precisely does the transition
to actuality occur, and what sort of causality is responsible for it?''.
All these hypotheses follow Heisenberg's recommendation that, although
measurements result in actualities, it is `during the physical, not the
psychical act of observation'12.1.
Faber discusses seven simple schemes as follows; the eighth I have added
to his list.
1. Actuality from present or future connections to our senses
This suggestion would resolve the problem of measurement, by ensuring that
whenever any set of outcomes will lead to different interactions with
human senses, then one of those outcomes will actually occur. Presumably
this will also apply for the senses of non-human sentient beings, but what
about experiments controlled by computers? One can easily imagine
(elaborating on possibilities described in Deutsch [1986]) that there are
situations where a computer has been programmed to make a measurement, but
not to tell us, or anyone, the actual result. According to this first
scheme, the whole computer would have to be in a superposition of states,
and could never be said to have definitely gone into a state of having
registered any outcome as distinct from any opposing outcomes. It seems
peculiar to have objective actualising conditions depend on some ultimate
outcome connected with sentient perceptions: I doubt that this connection
could be made sufficiently definite. It would also be hardly a
`materialist' theory if there were dependencies of this sort.
2. Actuality from Composite Objects
Perhaps individual particles follow the laws of quantum mechanics, but
the complexity of composite systems means that irreversible phenomena
occur which are equivalent to the actualisation of one of a selection of
possibilities. The difficulty here is in specifying the necessary degree
of complexity, for composite objects that are quite complex
have been observed to show quantum diffraction and interference
effects. Whole atoms and molecules show interference oscillations in one
and two slit experiments, and (as discussed in chapter
11,)
large crystals can interact with particles without specific or actual
interactions with any single atom in the crystal. It therefore appears
that compositeness, by itself, is not a sufficient condition for the
actualisation of propensities.
3. Actuality from Macroscopic Objects
All the known cases of actualisation of propensities, as observed to occur
with ordinary physical measuring apparatus, involve large or macroscopic
objects. Perhaps it is sufficient for actualisation that macroscopic
objects be involved: perhaps there is a new law of physics which says that
macroscopic properties, for example, cannot be in a superposition of
possibilities, but must settle for one option or another. Experiments
certainly don't rule this out, for it is a `minimal inductive
generalisation' of the type of experiments that have already been
performed, but, as Faber [1986] points out, it is a rather odd and ad
hoc hypothesis. We would be much happier if we had some physical
criterion, preferably from general principles, which distinguished
those properties which are sufficiently `macroscopic' from those which are
not. This criterion would have to allow such `large' systems as lasers and
superconducting metals to be in un-actualised quantum states, while
allowing some quite small systems, such as micro-electronic integrated
circuits, to be in definite and actual states.
4. Actuality from Alternative Interactions
Perhaps, whenever a quantum particle can interact with any of a number of
other systems, it ends up with actually interacting with only one (or
none) of them.
Bussey [1984], [1986] proposes, for example, that wave packet reduction (i.e.
actualisation) occurs during particle-particle interactions whenever
`individual atoms change state'.
This is similar to the hypothesis considered in chapter
11 ,
concerning whether all interactions could be actual events, and hence had to
definitely occur or not occur. We saw there that it could not be true, as
there is good experimental evidence (the crystal diffraction case, for
example) that interactions can occur without actualising. Bussey tries to
meet this objection by holding that when atoms bound together in a crystal
form a compound system, such systems behave as individual
quantum-mechanical entities in their own right. The crystal `as a whole'
does not change state after the diffraction, or at least not its internal
state (if Bussey were to make this distinction properly), and hence does
not produce actualising. The difficulty is that there is considerable
arbitrariness in what exactly constitutes a `compound system'. Ordinary
quantum mechanics does not draw any sharp distinction between compound
systems and fortuitous clusters of particles with energies near
bound-state
12.2
or resonance energies.
5. Actuality from Irreversible Interactions
The actualisation of propensities seems intimately connected with the
occurrence of irreversible processes. Perhaps actualisations are just the
consequence of irreversible events? The trouble with this option is
finding a definition of `irreversible events'.
One could attempt to base irreversibility on thermodynamics, such as its
Second Law. An irreversible event could be one during which entropy
increases. But is an increase of entropy an objective process, or is it a
consequence of our necessarily incomplete knowledge, and of our use of
probabilities to represent out ignorance?
Heisenberg [1958] advocated the use of thermodynamics and entropy to define
irreversible events, but in the end had to admit that irreversibility `is
a consequence of the observer's incomplete knowledge of the system and in
so far not completely ``objective''.'
My approach is to accept that propensity actualisations occur, and then
define irreversibility in terms of such events. As we saw in chapter
10,
however, some physicists have taken the opposite view, and hold that there
is an objective sense of `irreversibility', in large thermodynamic systems
for example, from which they can derive the irreversibility of
measurement events in the quantum domain.
Prigogine [1980, 1984] and Rae [1986] hold, for example, that
irreversible changes do not occur in quantum physics
specifically.
Rather, they occur principally in large complex systems in which there are
sufficient instabilities that `chaotic behaviour' follows. This means that
any arbitrarily small change in a starting condition will
result in completely different future behaviour. Their theory, however,
does not remove the need for some non-local phenomena in the
universe. Furthermore, although it declares that there is a transition
between the reversible quantum world and the irreversible thermodynamic
world, it does not say exactly at what point this transition occurs. Talk
of `large complex systems' merely brings back the problems of proposals 2
and 3 above. Until specific suggestions are made for the microscopic basis
of the supposedly fundamental `irreversible events', this proposal remains
a `philosophy of nature', rather than becoming a specific theory.
6. Actuality from Superpositions not inter-transformable
Schlegel [1980] has proposed that quantum superpositions can only contain
components that can be transformed into one another by what he calls the
`modified Lorentz group' (m.L.g.). These include the standard velocity
transformation, spatial translation and rotation, space but not time
inversion, and charge conjugation. This allows, for example, the
superposition of momenta of a whole crystal, but not the superposition of
unexposed and exposed photographic grains. The uncertainty, however, is
whether the m.L.g. applies to a whole system, or whether it applies
particle by particle. Schlegel does not want to apply to individual
sub-systems, to avoid the case of a photographic grain being transformed
by a series of steps, each of which is within the m.L.g. We suppose
therefore that we can only apply transformations to systems as a whole.
Consider, however, the case of a system (such as a neutron) decaying into
several particles with variable distributions of kinetic energy (as is the
case with the proton, electron and neutrino from neutron decay). Now
the Lorentz transformations needed to bring together all kinetic energy
combinations are all different, because transformations to different rest
frames are required. We would therefore predict that all continuously
different kinetic energies are actualised separately. This is
not observed experimentally, as it would mean that each observed outcoming
particle would be a wave packet of zero energy dispersion, and hence of
completely indeterminate time duration. It would also mean that there
could be no EPR-style non-local correlations between the various particle
spins.
7. Actuality from no general characteristic
Cartwright [1983] argues that there is no general
characteristic that describes the reduction of the wave packet (the
actualising of potentialities). Rather, it is a natural process that
happens all the time in many different ways. However, the examples she
gives of when actualisation is supposed to happen are not correct.
Actualisation does not necessarily occur at the point of decay
of radio-active nuclei or the preparation of an ion in a particular state
with a specific projection of its angular momentum in the direction of a
magnetic field, as in the Stern-Gerlach experiment.
All these schemes, Faber [1986] points out, are deficient in some way.
Some (such as nos. 1 and 5) turn out to not be sufficient definite in an
non-subjective sense for them to be objective conditions for
actualisation,
unless (after Prigogine and Rae) physical theory is deliberately extended
to provide the required objective sense. Others (such as nos. 2, 4, 6 and
possibly 7) are almost certainly wrong empirically: we know that nature
just does not behave like that. The remaining one (number 3) is somewhat
odd and ad hoc.
8. Actuality from point localisations in space and time
N. Maxwell [1976], in outlining a propensity interpretation of quantum
mechanics, suggested that actual events could be at specific points in
space and time, and hence amounted to position measurements of quantum
systems. All other kinds of quantum mechanical `observables' we taken to
be reducible to combinations of position measurements, as in Feynman and
Hibbs ([1965], p. 96). We have already seen in chapter
11 the deficiences in having point actualisations.
There are a group of proposals which suggest that there is a specific
duration of propensity fields before actual events occur.
In the language of quantum mechanics, they propose that there is a
specific duration of coherent superpositions before there is a reduction
of the wave packet.
These proposals are only partly elaborated, in that they still have free
parameters that have not been specified. Some of them refer to the
existence of hidden physical mechanisms which would have to be postulated,
but about which we know nothing as yet.
1. Actualisations outside a `correlation length'
One proposal for an `objective reduction of the wave packet'
comes from Einstein. In response to the difficulties in interpreting the
long-range correlations in his proposed EPR experiment, he suggested ``that
the current formulation of the many-body problem in quantum mechanics may
break down when particles are far enough apart.''12.3
There could then be a certain distance, such that particles separated by
more than this distance spontaneously reverted to statistical mixtures of
actual states, rather than remaining in superpositions. This prospect,
however, is made specific by Bell's inequalities (Bell [1964]), and
experiments have shown that there do remain non-local correlations between
quantum systems which may be separated by even large laboratory distances.
2. Actualisations from some `effective temperature'
Baracca, Bohm et al. [1975] propose that, due to some unavoidable couplings with
a `sub-quantum level', there is some `effective temperature' T for both
the sub-quantum and quantum systems, to reflect the equilibrium
distribution of energy. There would then be a `critical time'
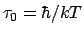 for the maximum duration of superposition
and correlations (k being Boltzman's constant). However, they do not
suggest any plausible values for this temperature. for the maximum duration of superposition
and correlations (k being Boltzman's constant). However, they do not
suggest any plausible values for this temperature.
3. Actualisations as localisation to gaussians wave-packets
Ghirardi et al. [1986] propose that there may be a new spontaneous process
of localisation of quantum wave functions, so that quantum substances end
up actually as one of a number of gaussian wave-packets. They choose the
parameters governing the rate of this process so that it happens more
rapidly, the more variables there are in the many-body wave function
 Benatti et al.
[1987] show how this ensures that large macroscopic pieces of measuring
apparatus very rapidly have one actual state, and not a superposition of
different states. Benatti et al.
[1987] show how this ensures that large macroscopic pieces of measuring
apparatus very rapidly have one actual state, and not a superposition of
different states.
Bialynicki-Birula and Mycielski [1976] considered adding a potential term
to Schrödinger's equation that is proportional to the logarithm of
the probability density:
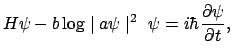 |
|
|
(12.1) |
then there are soliton-like solutions: wave functions which do not
continuously spread, but are stabilised with a finite extent
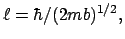 and hence could perhaps be taken to represent
particles and not just propensities for events. Here, H is the usual
quantum Hamiltonian, a is a constant for dimensional reasons, and b
is a positive constant with units of energy which determines the magnitude
of the non-linear effects. The non-linear soliton equation (12.1) was
not designed for the actualisation of potentialities, and does not give
proper selections of alternative branches of the and hence could perhaps be taken to represent
particles and not just propensities for events. Here, H is the usual
quantum Hamiltonian, a is a constant for dimensional reasons, and b
is a positive constant with units of energy which determines the magnitude
of the non-linear effects. The non-linear soliton equation (12.1) was
not designed for the actualisation of potentialities, and does not give
proper selections of alternative branches of the 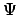 function, but,
as Shimony [1986] points out, it does allow us to quantify the departures
from ordinary quantum mechanics. Very accurate neutron diffraction
experiments have been
performed (see Zeilinger [1986]), and these have all supported ordinary
quantum mechanics, and to date have placed upper bounds on b of about function, but,
as Shimony [1986] points out, it does allow us to quantify the departures
from ordinary quantum mechanics. Very accurate neutron diffraction
experiments have been
performed (see Zeilinger [1986]), and these have all supported ordinary
quantum mechanics, and to date have placed upper bounds on b of about
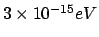 . This figure would mean that the soliton
solutions would spread to as large a diameter as 3 mm before being
stabilised by the non-linearities. It is remarkable, Zeilinger admits,
that even the nonlinear theory has to admit the existence of macroscopic
quantum objects. . This figure would mean that the soliton
solutions would spread to as large a diameter as 3 mm before being
stabilised by the non-linearities. It is remarkable, Zeilinger admits,
that even the nonlinear theory has to admit the existence of macroscopic
quantum objects.
5. Actualisations from statistical fluctuations in the Hamiltonian
If there were statistical fluctuations in the potentials appearing in the
quantum mechanical Hamitonian, Pearle [1976, 1986] points out that the
Schrödinger equation behaves like a diffusion equation. The
probabilities of different branches diffuse in a random walk and end up
either at zero or unity. In this way, the reduction process is the
physical product of an underlying `Brownian motion' in some physical
medium as yet unknown.
Bohm and Bub [1966] present a similar scheme.
We now come to a group of proposals which make specific numerical
predictions for the duration of propensity fields before actual events
occur. They do not contain any free parameters which could be arbitrarily
and independently adjusted, so we have here the beginnings of fully
fledged physical theories.
1. Actualisations from energy differences
The original proposal along these lines is that of Bedford and Wang
[1975], when they suggested that superpositions of states of energy
difference 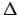 E only last for a time E only last for a time
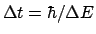 before spontaneously collapsing into actually one or other of the
states, in a statistical mixture. That is, interference oscillations
between states of different energy could only last for one cycle before
they became actually one particular state. Any measurement apparatus will
have alternative states different in energy, so all equipment will very
rapidly revert to actually be in just one of its states.
before spontaneously collapsing into actually one or other of the
states, in a statistical mixture. That is, interference oscillations
between states of different energy could only last for one cycle before
they became actually one particular state. Any measurement apparatus will
have alternative states different in energy, so all equipment will very
rapidly revert to actually be in just one of its states.
Bedford and Wang [1977] then realised that there are counter-examples to
this hypothesis. A photon originating in two radiotransmitters of
different frequency will interfere at distances beyond that predicted by
the criterion.
Quantum beat experiments (Andrä [1970]) show interference
oscillations lasting for many cycles without sign of abatement. Bedford
and Wang [1977] therefore revised their criterion, to have it necessary
for actualising that the several systems with energy differences must (a)
be in a state which has no factorisation (i.e. is not really an
uncorrelated product of two free fields), (b) be effectively
non-interacting, and (c) be relatively unaffected by environmental
fluctuations.
2. Actualisations from inelastic energy differences
N. Maxwell [1982] refined the criterion of Bedford and Wang, and only
allowed inelastic or rest mass energy differences to
give rise to actualisations. Inelastic energy differences 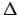 E are
those between two bound states and/or resonances of a given system. If the
system is treated as a compound whole, then it its rest mass m will
differ by E are
those between two bound states and/or resonances of a given system. If the
system is treated as a compound whole, then it its rest mass m will
differ by
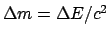 . Restricting the
actualising criterion in this way avoids the refutations of the Bedford
and Wang hypothesis above, but we still have to keep the `non-interacting'
condition. Maxwell proposes that the interval . Restricting the
actualising criterion in this way avoids the refutations of the Bedford
and Wang hypothesis above, but we still have to keep the `non-interacting'
condition. Maxwell proposes that the interval
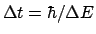 be counted from the cessation of any interactions, and so is
timed while there are no interference effects. The idea is that
if there have been interference effects, and then they disappear for a
whole cycle, actualisation then makes them disappear permanently. If there
was going to have been interference oscillations again, then actualisation
means that there is an experimental difference with ordinary quantum
mechanics. Maxwell [1982, 1986, 1988] proposes some crucial experiments,
though it would be rather difficult to set up the necessary coherent
arrangements. be counted from the cessation of any interactions, and so is
timed while there are no interference effects. The idea is that
if there have been interference effects, and then they disappear for a
whole cycle, actualisation then makes them disappear permanently. If there
was going to have been interference oscillations again, then actualisation
means that there is an experimental difference with ordinary quantum
mechanics. Maxwell [1982, 1986, 1988] proposes some crucial experiments,
though it would be rather difficult to set up the necessary coherent
arrangements.
Maxwell [1986] recognises that his criterion will have to be generalised
to allow for (a) multiple inelastic states, (b) a statistical half-life of
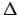 t, rather than a fixed duration, and (c) the gradual cessation of
interactions, as coupling potentials never cut off absolutely. t, rather than a fixed duration, and (c) the gradual cessation of
interactions, as coupling potentials never cut off absolutely.
3. Actualisations from gravitational differences
Penrose ([1986], [1987]), after considerations of various problems in
cosmology and quantum gravity, thinks that wave function collapse is
linked with gravitation.
When two states of differing energy distribution are linearly superposed,
the slightly differing space-time geometries that these energy
distributions produce (according to general relativity) must also be
superposed. 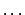 I would contend, therefore, that when two geometries
involved in a linear superposition become too different from one another
-- in some yet-to-be-determined precise sense -- then linear
superposition fails to hold, and some effective non-linear instability
sets in, resulting in one or other geometry winning out, the result being
reduction I would contend, therefore, that when two geometries
involved in a linear superposition become too different from one another
-- in some yet-to-be-determined precise sense -- then linear
superposition fails to hold, and some effective non-linear instability
sets in, resulting in one or other geometry winning out, the result being
reduction
Penrose [1986] originally thought that wave functions collapse when the
the apparent lowering of entropy that such a process leads to is more than
compensated by the rise in some kind of gravitational entropy. It could
then be allowed as consistent with the Second Law of thermodynamics (that,
in all processes, entropy must either increase or remain constant). He
then added in postscripts that the criterion should be phrased in terms of
the more clear-cut `graviton number'. On that view, ``wave function
collapse takes place when the difference between the gravitational fields
of the states under superposition amounts to at least one graviton's
worth''. According to his calculations, this means that `actualisations'
occur for droplets of water with diameters of around 10-5 m,
which is sufficiently small for nearly all measuring apparatuses to have
definite states rather than superpositions.
Similar ideas are put forward by Károlyházy et al [1986],
who also consider the uncertainty in the spacetime metric predicted in
general relativity if there were uncertainties or superpositions of energy
distributions. They calculate the reduction rate, assuming that it occurs
when uncertainties in the metric imply that the wave function 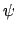 propagates with uncertainties of up to half a cycle (i.e. a phase
uncertainty of
propagates with uncertainties of up to half a cycle (i.e. a phase
uncertainty of 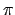 ). They do not know why or how wave packet reductions
occur: they can only estimate very approximately how often they are likely
to happen. Their conclusions are that atoms and nuclei have negligible
probability of actualising in the known lifetime of the universe, but a
ball of 1 cm diameter and terrestrial density will reach its phase
uncertainty of ). They do not know why or how wave packet reductions
occur: they can only estimate very approximately how often they are likely
to happen. Their conclusions are that atoms and nuclei have negligible
probability of actualising in the known lifetime of the universe, but a
ball of 1 cm diameter and terrestrial density will reach its phase
uncertainty of 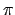 within 10-4 s, and hence behaves as a
classical object as expected. The largest uncertainties before actualising
sets in are found to be for masses of 10-14 g: that of a
colloidal grain, containing within 10-4 s, and hence behaves as a
classical object as expected. The largest uncertainties before actualising
sets in are found to be for masses of 10-14 g: that of a
colloidal grain, containing
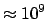 molecules, for which
actualisations should occur only several times per hour. They proposal two
experiments, preferably to be performed in weightless conditions in a
space laboratory. molecules, for which
actualisations should occur only several times per hour. They proposal two
experiments, preferably to be performed in weightless conditions in a
space laboratory.
From the point of view of experimental evidence to date, all three of
these quantitative proposals are equally satisfactory. The Bedford and
Wang proposals, however, are not as accurately formulated as they could
be: the non-factorising and non-interacting conditions, they point out,
have to be interpreted in an approximate rather than a precise sense. The
second two proposals are more definite in their application, but are quite
different from each other in their predicted rates of actualisation. N.
Maxwell's proposal has actualisations happening quite quickly at every
nuclear, atomic and molecular level. Because of his condition that timing
starts only after interactions cease, however, the effects of actualising
(the predicted losses of coherence) will be almost impossible to detect in
practice. If his proposal is modified to allow for some kind of
`progressive probability' for actualising as interactions progressively
fall away, then there will be small but definite effects in a variety of
scattering experiments. Such modifications are eagerly awaited.
The proposals of Penrose and of Károlyházy predict a much
slower rate of actualising. They allow wave packets to become quite large
(on a molecular scale) before some gravitational differences trigger an
actualising localisation again. Penrose does not see his process as
`actualisation' at all, but as the symptoms of some new `non-linear
instability' that might occur in other physical circumstances too. That
is, he is still looking for some microscopic mechanisms which underly the
quantum phenomena. Following Bell's Inequalities, of course, these will
have to be non-local phenomena, but Penrose has not begun to publish any
specific thoughts in this direction.
One consequence of adopting one of the quantitative proposals of this
section, is that there can then be a new objective sense for
some of the notions proposed in the previous section for actualising. That
is, if Maxwell, Penrose or Károlyházy proved to be correct,
then we could find new objective meanings for the notions of `composite
object', `macroscopic object', `alternative interactions' and
`irreversible processes'. These could all be redefined in terms
of some new objective process of actualising. This is particularly useful
in the case of `irreversible processes', as then we would have a new
microscopic foundation for thermodynamics.
In both classical and quantum physics, Prigogine [1980] points out, the
reversibility of the microscopic laws makes it difficult to have a `real
thermodynamics' with objective definitions of irreversibility and entropy,
etc. If an `actualising' process were found to be fundamental, then a
variety of objective proposals for an `entropy superoperator' could be
considered (see Prigogine [1980], p. 168 for one such proposal).
Thermodynamics could then be put on a new footing.




Next: 12.3 Mind-dependent Actualisation -
Up: 12. Measurements and Other
Previous: 12.1 The Problem of
Prof Ian Thompson
2003-02-25
|
![]()