|
| |




Next: 10.3 Waves, Particles and
Up: 10. Quantum Substances
Previous: 10.1 Classical and Quantum
Subsections
10.2 Probabilities and Propensities
In the early development of quantum physics, Born realised that the
quantum theory did not predict the precise state after a collision, but
only the `possibility of a definite state' (Born [1926]). The wave fields
were not actual fields, but only determine the probability of the presence
of quanta. What is new in the quantum theories is this emphasis on
probabilities. In his `ensemble interpretation' of quantum
mechanics, Born tried to take these probabilities as relative
frequencies in an ensemble. An `ensemble' here is a real or imagined
collection of systems that are as similar as we can make them. The
probabilistic nature of quantum mechanics means that not all systems in
the ensemble will behave in the same way, and only the relative numbers of
the different outcomes is predicted from quantum theory. The ensemble
interpretation of probabilities leaves quite open the significance of
probabilities for individual systems:
the `propensity' notion of probability (see chapter
2)
is designed to provide just such a meaning for attribution of
probabilities to single systems. Even if we are have only one radioactive
atom, for example, surely some meaning can be given to the likelihood of
the decay event occurring in different intervals of time.
Heisenberg
Jammer [1966, p. 286] relates how
Laws of nature, as Born and Heisenberg contended  determined not the occurrence of an event, but the probability of the
occurrence. For Heisenberg, as he later explained it
10.1
, such probability wave are ``a quantitative formulation of the
concept of `dynamis', possibility, or in the later Latin version,
`potentia', in Aristotle's philosophy. The concept of events not
determined in a peremptory manner, but that the possibility or `tendency'
for an event to take place has a kind of reality - a certain intermediate
layer of reality, halfway between the massive reality of matter and the
intellectual reality of the idea or the image - this concept plays a
decisive role in Aristotle's philosophy. In modern quantum theory this
concept takes on a new form; it is formulated quantitatively as
probability and subjected to mathematically expressible laws of nature.'' determined not the occurrence of an event, but the probability of the
occurrence. For Heisenberg, as he later explained it
10.1
, such probability wave are ``a quantitative formulation of the
concept of `dynamis', possibility, or in the later Latin version,
`potentia', in Aristotle's philosophy. The concept of events not
determined in a peremptory manner, but that the possibility or `tendency'
for an event to take place has a kind of reality - a certain intermediate
layer of reality, halfway between the massive reality of matter and the
intellectual reality of the idea or the image - this concept plays a
decisive role in Aristotle's philosophy. In modern quantum theory this
concept takes on a new form; it is formulated quantitatively as
probability and subjected to mathematically expressible laws of nature.''
Unfortunately Heisenberg does not develop this interpretation much beyond
the sort of generality of the above statements, and the concept of
`potentiality' remains awkwardly isolated from much of his other thought
on this subject
10.2
.
It is unclear even what he means by `potentia'. Herbert
[1985], in describing Heisenberg's ideas, imagines them to be more
emphemeral than substantial:
Heisenberg's half-real universe of potentia is reminiscent of certain
oriental views developed in contexts far removed from quantum physics:
This floating world is but a phantasm
It is a momentary smoke
Though ghostly and transitory, Heisenberg's shimmering ocean of potentia
is the sole support for everything we see around us. The entire visible
universe, what Bishop Berkeley called ``the mighty frame of the world,''
rests ultimately on a strange quantum kind of being no more substantial
than a promise
10.3.
We will see below that, far from being as emphemeral as a promise, the
propensities of the physical world are perfectly real and substantial.
They are in fact the very substances out of which all things are made.
The present concept of `continuant' is also very similar to Nicholas
Maxwell's notion [1982, 1985, 1988] of smearon or
propensiton.
``Smearons'', as understood here, are hypothetical fundamental physical
entities, having characteristics somewhat like the ``wave packets'' of
orthodox QM in being smeared out in space like a wave function, but being
unlike orthodox wave packets in having physically real nonlocal
characteristics that in general exist in space and evolve in time
independently of methods of preparation and measurement. What is smeared
out in space is the propensity of one smearon to interact in a
probabilistic, quasiparticle-like way with another smearon, should the
appropriate physical (smearon) conditions to do so arise. The state
vectors of QM are to be interpreted as characterising the actual physical
states of smearons. The physical states of smearons evolve
deterministically, in accordance with Schrödinger's time dependent
equation (for elementary QM) as long as no probabilistic particle-like
interactions between smearons occur. Probabilistic particle-like
interactions between smearons involve changes of state which violate
Schrödinger's time dependent equation even though no measurement
is made. If appropriate physical conditions arise for an unlocalized
smearon, in a state  , to interact in a probabilistic way with just
one of many other highly localized smearons, then, roughly speaking, the
probability that the unlocalized smearon interacts with the smearon
LOcalized in dV is given by , to interact in a probabilistic way with just
one of many other highly localized smearons, then, roughly speaking, the
probability that the unlocalized smearon interacts with the smearon
LOcalized in dV is given by
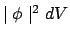 (this
being a microrealistic reformulation of Born's original [1926]
probabilistic interpretation of wave mechanics, which appealed explicitly
to measurement). Smearon QM is thus a theory that is, in the first
instance, exclusively about how smearons physically evolve and interact
with one another in space and time independently of preparation and
measurement. Measurements are probabilistic interactions between smearons
which just happen to be recorded by physicists. Stable macro objects are
the outcome of many probabilistic interactions between smearons.
(Maxwell [1982] p. 609) (this
being a microrealistic reformulation of Born's original [1926]
probabilistic interpretation of wave mechanics, which appealed explicitly
to measurement). Smearon QM is thus a theory that is, in the first
instance, exclusively about how smearons physically evolve and interact
with one another in space and time independently of preparation and
measurement. Measurements are probabilistic interactions between smearons
which just happen to be recorded by physicists. Stable macro objects are
the outcome of many probabilistic interactions between smearons.
(Maxwell [1982] p. 609)
The causal analysis of section 7.2 can therefore be used to
provide a philosophical justification and elaboration of the idea of
smearons or propensitons, where it is remembered that propensitons only
localise themselves intermittently.




Next: 10.3 Waves, Particles and
Up: 10. Quantum Substances
Previous: 10.1 Classical and Quantum
Prof Ian Thompson
2003-02-25
|
![]()