|
| |




Next: References
Up: 13. Summary of the
Previous: 13.2 When actualities at
13.3 When actualities are selections of alternatives
- Principle of Selection
- the effects of the actualisation are a selection of the field extent
not only at the time of the actualisation, but also at all subsequent
times.
- Derivative Dispositions
- Actual events are produced in a two-stage process, with the
propensities for the actual events themselves being derivative
from the propensities for virtual events.
- Two Stages of Propensities
- First there are `free-field propensities' (satisfying equation
(11.1)), and these interact by means of virtual events to produce
many-body wave functions
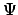 (satisfying equation (11.2), or
its replacement in relativistic quantum field theory). These many-body
wave functions then describe the propensities for actual events, which are
selections from within the range of the (satisfying equation (11.2), or
its replacement in relativistic quantum field theory). These many-body
wave functions then describe the propensities for actual events, which are
selections from within the range of the 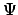 -function satisfying the
Principle of Selection. -function satisfying the
Principle of Selection.
- Space for Virtual Events
- is marked not by definite positions, but by equivalence
classes of sets of positions, all of which are `essentially the
same' as far as the production of actualising propensities is concerned.
- Gauge Invariances
- Extensiveness in the space for virtual events is relational
in a real (absolute) sense. This relational structure can be equivalently
formulated as the `gauge invariance' of all physical laws with respect to
choices within the following equivalence classes:
-
- 1.
- Interactions imply extensive relations in space and time,
rather than definite and absolute positions. It makes no difference to
any interaction or event if the whole universe were to be shifted over in
space, or delayed arbitrarily in time, or rotated about any axis.
- 2.
- Interactions use potentials which are arbitrary with respect to additions
of certain kinds of spatio-temporal functions, and hence generate
complex-valued wave functions which have a corresponding arbitrariness in
their phase.
- 3.
- Interactions in quantum field theory operate in arbitrarily small regions
of space-time, and hence almost always need a variable renormalisation to
correct the self-energies (i.e. masses) of the particles, and to correct
the coupling-strengths of the interaction terms.
- 4.
- Interactions can be between identical particles, for which, as
they can be arbitrarily interchanged, we need to apply the Pauli Exclusion
Principle.
- Unchanging Continuant (Substance)
- is field of propensity for virtual (not actual) events.




Next: References
Up: 13. Summary of the
Previous: 13.2 When actualities at
Prof Ian Thompson
2003-02-25
|
![]()