|
| |




Next: 8.3 Past and Future
Up: 8. A Theory of
Previous: 8.1 Possibilities as Places
Subsections
8.2 Extensiveness, Space and Time
In the previous section, places in spacetime were defined as possibilities
of a certain kind. The question to be asked next is how these places are
`brought together' to form one world with continuous space and time. We
want to know how the particular things in the world can be at different
places, yet stand in definite relations to one another. We must also
consider the question of the ontological status of space and time: whether
they are absolute, relative, and whether space and time exist separately
from a joint `space-time' which may be formulated.
In the previous chapter, it was remarked that not all places could be
identical, as then it would be impossible to have any separate existences
or variety in the world. Neither should we go to the other extreme, and
have all places distinct but with no real relation to each other.
Both Leibniz and Bergson tended to this extreme when they tried to deny
the reality of extension.
We may observe, very generally, that a particular thing will tend to act
on (and be changed by acts of) other particulars which are `nearer',
rather than those which are `further away'. To explain this fact, some
kind of extensiveness is necessary. There must be some kind of `real
extensiveness' which is related to how particulars can interact with each
other (and not merely some kind of `phenomenal space' that only describes
how things appear to us).
Some philosophers, such as the pre-critical Kant8.2, or Bergson perhaps, have tried to derive extension from
these mutual interactions. In Kant's doctrine of acting monads, extensive
relations were brought into being by the acting of the monads on each
other, because each monad `fills an assignable space' by its intrinsic
activity.
The trouble with this approach, as Leclerc8.3
points out, is that the very fact of the mutual interacting of distinct
substances presupposes that the participants are in some sense
`other' to each other. Thus extension must be necessarily prior to any
mutual interacting.
Whitehead points out that extension has the double role of allowing for
the externality of distinct places while, at the same time, bringing them
together by means of geometrical and chronological co-relations:
``extensive connection with its various characteristics is the fundamental
organic relationship whereby the physical world is properly described as a
community''8.4.
Extensiveness and the Extensive Continuum
Extensiveness is therefore defined, in the present philosophy
of nature, as a fundamental real relation between places.
It is a relation between places that holds independently of whether or not
the related places are filled. We could think of it specifying absolutely
the metric distance between any two points in space-time.
By means of extensiveness we intend to create a `dimensional order' for
all places in space and time. Furthermore, since places are kinds of
possibilities, and since (as we saw in chapter
6) possibilities can form a continuum, we have that extensiveness can
naturally give rise to a continuous order of places. I am not arguing
that extensiveness is necessarily continuous, only that continuity is not
incompatible with the basic notions we have put together. We will discuss
later how all places can be ordered according to their mutual extensive
relations.
When this is done, they then form what Whitehead has termed an
`extensive continuum'. This continuum is the manifold of all places
apparent when they are juxtaposed with respect to their relations of
extensiveness. The extensive continuum is the most general form of order
in the world, as it is prior to the contingent things which actually
happen. It is not however to be conceived as actuality, or as
any kind of definite `container'. As the full definition of the extensive
continuum is that it is an `ordered manifold of places', it is therefore
the `continuous order of possibilities for actuality'. It would only be if
we erroneously conflate the concepts of possibilities a we would mistake
the extensive continuum for an actual entity. Such conflation may be
permissible within mathematics, but has disastrous consequences elsewhere.
In understanding the extensive continuum in terms of our usual space and
time, we should remember the places, as possibilities for actuality,
are `wheres' and `whens'. This means, as pointed out at the start of the
chapter, that the extensive continuum has more of a spatiotemporal nature,
than of a purely spatial or purely temporal nature. We can refer to the
extensive continuum as `spacetime', but only provided we remember that
such a spacetime is not the actual existent of many
interpretations of Einstein's relativity theories. Rather, it is the
extensive manifold of all possibilities for actuality. On this
basis we can admit the `objective' nature of the four-dimensional
spacetime of relativity theory, but not as an actual or fully-determinate
thing.
Metrics
Extensiveness has been defined as a relation between places, but we have
still to see how it may be more precisely formulated. We might expect,
because extensiveness can be continuous, that places can be related a
`continuous relation'. Mathematically this could be represented as a
function s(p,q), as a continuous function of pairs of places
p, q. Our general philosophy of nature cannot determine the exact
form of this function, for to know its characteristics would be to know
the number of dimensions of space and time in spacetime, and to know the
precise metric of the spacetime manifold.
I see no way of deriving these a priori. The 3+1 dimensional
nature of spacetime, for example, seems to be a `brute fact'. Both the
Newtonian and Einsteinian accounts of spacetime should however be
permitted by our general philosophical arguments. In the following, I
will hence be discussing a plausible formulation of extensiveness which
can accommodate both Newtonian and relativistic metrics.
It is supposed that the extensiveness function is given as the function
s(p,q) for all pairs of places p & q, such that
-
- 1.
- s2(p,q) is real-valued,
- 2.
- s(p,p)=0 for all places p,
- 3.
-
s(p,q) = - s(q,p) for all p, q, and
- 4.
-
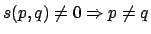 (though (though
 ) )
These are just the preliminary relations which are supposed to be
satisfied. The more useful relations `p precedes q' and `p
alternates with q' are now defined by
| p precedes q |
 |
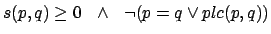 |
(8.1) |
| p alternates with q |
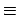 |
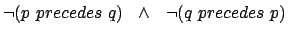 |
(8.2) |
| |
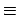 |
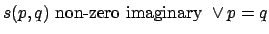 |
(8.3) |
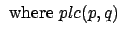 |
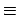 |
 |
(8.4) |
The relation plc(p,q) is a special condition necessary with
relativistic metrics to mark the case of p being on what is called the
`past light cone' of q An inverse relation succeeds can
also be defined:
In relativistic physics, precedence is known as the `time-like' or
`topological past' relation, and alternation as the `space-like' or
`topological present' relation between two places. This correspondence
obtains because the form of the relation s(p,q) that is used
above is based on the characteristics of a differential metric that could
be either the relativistic
ds 2 = c2 dt2 - dx2 - dy2 - dz2 ,
or that developed from Newtonian space and time:
In our case, however, the extensiveness s(p,q) is definite for
pairs of places even if the particular coordinate allocation of
 is dependent on the choice of some observer. is dependent on the choice of some observer.
Momentum Space?
From the mathematical point of view, an function
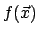 over the
coordinates over the
coordinates
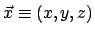 can be equivalently expressed as a
function can be equivalently expressed as a
function 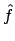 over momentum space over momentum space
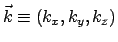 using the Fourier transformation using the Fourier transformation
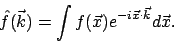
All the information present in
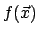 is also present in is also present in
 Schrödinger's equation (among others) can be
expressed equally as well in momentum space as in ordinary space, so it
is not clear in quantum mechanics which space is the `more real'. Schrödinger's equation (among others) can be
expressed equally as well in momentum space as in ordinary space, so it
is not clear in quantum mechanics which space is the `more real'.
In the philosophy of nature, the question of which space is the `real'
space can be decided by means of the argument used above to introduce
space in the first instance. The mutual interaction of distinct substances
presupposes that they are in some sense `other' to each other, and hence
there must be a real extension or a real space which is necessarily prior
to any mutual interacting. A space is therefore real if that kind of
spatial proximity is the prerequisite for interactions. On the basis of
this criterion, ordinary space is real compared with momentum space. The
`process logic' can be applied equally well to both spaces, but
interactions tend to be local in ordinary (rather than momentum) space.
Thus proximity in momentum space is not of itself a necessary condition
for interactions occurring, and hence momentum space is not a `real
space' for processes and propensities.




Next: 8.3 Past and Future
Up: 8. A Theory of
Previous: 8.1 Possibilities as Places
Prof Ian Thompson
2003-02-25
|
![]()
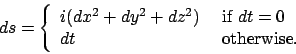
![]() over the
coordinates
over the
coordinates
![]() can be equivalently expressed as a
function
can be equivalently expressed as a
function ![]() over momentum space
over momentum space
![]() using the Fourier transformation
using the Fourier transformation