|
| |




Next: 8.2 Extensiveness, Space and
Up: 8. A Theory of
Previous: 8. A Theory of
Subsections
8.1 Possibilities as Places in Space and Time
We saw in chapter
7
that for an actual event A to cause an actual event B, there was a
set of possibilities for the change. This set may have members
apart from the possibility for B, and its members form a `space-time'
of possibilities for change, only one of which actually occurs.
We can now identify (following Leclerc [1972]) places in
space-time as just these `possibilities for actuality'. We can then
say that the event is at a place when that possibility is being
realised, and that this results in that place being `filled'. Since what
is actual is at least possible, the set of filled places is a changing
subset of the set of all places possible in the world.
These places are being regarded as `wheres' and `whens'. That
is, in the terminology of modern physics, places are places in space-time,
not just in space. This is especially important if these places are to be
the possibilities for events, for two events at different times, even
though perhaps at the same spatial location, are always distinct: they
realise different possibilities. This consideration is independent of any
requirements of relativity theory, as it can be used with both Newtonian
and Einsteinian space and time.
If the events being considered are ordinary physical events such as
interactions, collisions, etc., in our everyday three-dimensional space
and time, then places (as `possibilities for these
events') can be identified with distinct regions of spacetime. The
relational structure of implication no. 5 can be identified with the
metric tensor that gathers regions into subsets of some larger space-time
continuum.
The theory of spacetime being developed here is similar to that of
Whitehead's `extensive continuum', which is the `coordination of all
possible standpoints'.
Whether this is an `absolute' or `relative' view of spacetime depends on
how particular possibilities are individuated and identified. This is
discussed in subsection
8.2,
and further in chapter
11.
The events however need not be in our usual space and time: the analysis
is quite general. Quantum mechanics postulates, for example, that
particles with intrinsic spin have this spin `oriented' in a
`spin space' distinct from our three dimensional space, and
not simply embedded in it. Moreover, intrinsic spins have only
a discrete range of possibilities. According to the process
analysis of this paper, this is equivalent to saying that the spin can
only range over a discrete set of `positions' or `places'.
These places would be related to each other, in this case, as integers, or
half-integral numbers.
Point Places in Which Space?
In chapter
6,
we saw that pure actualities had to be unextended and indivisible.
Places, as possibilities for these actualities, must therefore also be
unextended and indivisible, and hence must be points in space-time. The
analysis so far, however, is quite general: we have still not said exactly
which space-time we are considering. For a preliminary model of
the process logic, consider the places to be points in our ordinary
three-dimensional space along with its one-dimensional time. Actualities
are therefore produced by point events in our four-dimensional spacetime,
and hence have unique locations describable by coordinates 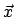 and
t in the usual fashion. and
t in the usual fashion.
It is not logically necessary for actual events to be points in ordinary
space and time, but this is a `contingent identification' between our
theory and its application. This contingency follows the same pattern we
found previously for dispositions in section 2.6, for mathematics
in chapter
6,
and for general philosophies of nature in chapter
5.
In chapter
11,
we will consider an alternative identification of what is actual,
and thus an alternative identification of the `space-time of places'
wherein actualities are at single points.
On Real Possibilities
It is essential to remember that `places' are realistic
possibilities, and are not merely abstract or de dicto
possibilities such as those which arise when we might think or form
propositions about what is possibly the case.
Rather, we want here to have possibilites for physical events:
possibilities which are relevant to what actually occurs. A great many
de dicto possibilities are perfectly capable of being
rationally entertained, but are nevertheless never possibilities for
actualisation, either because they are not within the scope of physical
laws, or because they are ruled out by the path that history has taken up
to the present.
The `possibilities for events' are not de re possibilities
either. For de re possibilities involve particular objects, and
here, the `possibilities for an event B' are distinguishable even if
no such event occurs or exists in any way.
Following the arguments of chapter
7,
they are certainly not `possible events', or any kind of events which in
some way `subsist' without actually existing.
As Quine indicates, there are decided problems with the the
notion of `possible entities'. Taken together, they seem to be part of an
`over-populated universe'. ``Take, for instance, the possible fat man in
the doorway; and, again, the possible bald man in that doorway. Are they
the same possible man, or two possible men? How can we decide? How many
possible men are there in that doorway?''
8.1
There are severe problems for the application of
identity-criteria to `possible entities', but not to the
`possibilities for entities' discussed above. A `possibility
for a fat man in the doorway', for example, is just any one
of a number of regions in the doorway at some particular time, and these
are identified and individuated by the usual spatio-temporal relations in
an unambiguous fashion. The doorway may well contain a possibility for a
fat man and/or a possibility for a bald man, but that does not
require that we identify and individuate these `subsisting' men. We
only need to identify the places which would be occupied if
such men were to exist.
Finally, the `possibilities for events' are not reducible to talk
of `possible worlds', especially since I am interested in what
possibilities there are in and for this world. According to the
usual theory of `possible worlds', the actual world is just one possible
world, to be selected by a knowledge of what actually happens at all
times. Knowledge of which actual world we are in, therefore, is equivalent
to knowledge of all past and future events.
Any indeterminism in nature must be only a certain `looseness' in the laws
that link events at different times, and cannot be linked to any different
ontological status between the past and the future. I want to
have a natural ontology in which actualities only exist for past
events, with none for any future events. It is difficult to accommodate
this ontology within the framework of a `possible worlds' theory of
modality. It could only be done by making each temporal state of each
possible world to be the set of all past events up to that time.
Even if I do not use this formulation, I can still talk of futures
`accessible' at a given time, given the past history up to that time.
I argue, however, that these futures are part of our one present world,
and, moreover, are present only as possibilities, not in full actuality.
The important thing is to take possibilities seriously, and not to confuse
them with actuality. We saw in chapter
6
how, from the mathematical point of view,
possibilities and actualities could be all grouped together in a one-level
universe of Fregean `objects'. In mathematics, however,
no distinctions are made between actualities and possibilities: from the
point of view of extensional semantics, possibilities are just as much
`objects' as actualities. This does not mean that, properly
considered, actualities cannot be the realisation of possibilities.
We have seen previously how Whitehead warns against
the mistake of confusing mere potentiality with actuality.




Next: 8.2 Extensiveness, Space and
Up: 8. A Theory of
Previous: 8. A Theory of
Prof Ian Thompson
2003-02-25
|
![]()