|
| |




Next: 11.2 Actual and Virtual
Up: 11. Two Stages of
Previous: 11. Two Stages of
Subsections
11.1 Point Events
Up to now we have been constructing a philosophical framework for the
earliest kind of quantum mechanics, and have not paid any special
attention to interaction events. The actualising events considered so far
have been simpler, and more like the spontaneous acting of a single
homogeneous propensity field.
This field could reasonably be imagined to follow Schrödinger's
equation, but we have not decided between whether the Schrödinger
wave function is for `free field' substances (between interactions), or
whether it is a many-body wave function including interaction
potentials. The free-field equation for the p'th substance could be
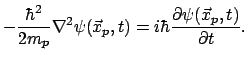 |
|
|
(11.1) |
Interaction potentials of the form
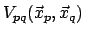 between substances p and q mean that the
many-body wave function between substances p and q mean that the
many-body wave function
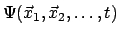 could satisfy the Schrödinger's equation could satisfy the Schrödinger's equation
![$\displaystyle \sum_p [ - \frac{\hbar^2}{2m_p} \nabla ^ 2_p \Psi
+ \sum_q V_{pq} (\vec{x}_p , \vec{x}_q) \Psi ]
= i \hbar \frac{\partial \Psi}{\partial t} .$](img81.gif) |
|
|
(11.2) |
The potentials Vpq may describe electromagnetic,
gravitational or one of the stronger nuclear interactions.
The wave function needs to be defined over the configuration
space
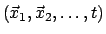 of all
possible places for interactions, as mentioned in chapter
4,
since all the interacting substances will in general have propensities for
actualisation that are correlated with each other (in the EPR sense),
because of previous interactions. Equations (11.1) and (11.2) are
the Schrödinger form of quantum mechanics, but the same propensity
distributions between times t1 and t2 could
equally well be described in the Heisenberg representation,
or in terms of a Lagrangian density of all
possible places for interactions, as mentioned in chapter
4,
since all the interacting substances will in general have propensities for
actualisation that are correlated with each other (in the EPR sense),
because of previous interactions. Equations (11.1) and (11.2) are
the Schrödinger form of quantum mechanics, but the same propensity
distributions between times t1 and t2 could
equally well be described in the Heisenberg representation,
or in terms of a Lagrangian density
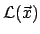 subject to a
least action principle subject to a
least action principle
 |
|
|
(11.3) |
For a particle of mass m in a potential
 , the Lagrangian
density (to be subject to variations in , the Lagrangian
density (to be subject to variations in
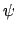 and and
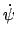 ) is ) is
Whether propensities contained interactions or not, point
actualisations were assumed to occur, whereby they became momentarily
localised at a point in spacetime. After that actual localisation, the
field dispersed again according to one of the Schrödinger's
equations above, and continued spreading out (for some finite time
interval) until the next localisation event.
These localisations fulfilled the role of `measurement events' in ordinary
QM, in being definite choices and having definite characteristics once
they occurred.
As in N. Maxwell [1976], measurement processes in quantum physics were
held to essentially involve these localisation events, and all kinds of
measurements of different physical variables were held to be ultimately
reducible to different combinations of `position measurements' in our
actual localisation processes. Measurements are not assumed to essentially
involve any conscious observer, but could be done by computer for example,
as the localisation events were a spontaneous natural process that
occurred because of the very nature of quantum substances as fields of
propensity for actual events of that kind.
Can all interactions be actual events?
If we consider the first option, wherein the propensity fields describe
substances while they are not interacting, then interactions must arise
because of the actualising events. The actual events are thus the
interacting, or the acting of one propensity field on another.
As Leclerc [1972, ch. 23] points out, `actings on' always involve a
reciprocal capacity to `receive' in that which is acted upon, so
that aspects of capability or propensity are required in both the agent
and in the patient. That most events are interactions is also supported
by quantum physics, where events which are the spontaneous action of a
single particle are comparatively rare, because events such as spontaneous
decays are not the most common type.
Figure:
Successive Localisations of Propensity Fields via Overlap Interactions
 |
If an interaction between two propensity fields is to result in
an actual event at a particular place, it will be necessary for the two
propensity fields to overlap in at least that region.
This would be a generalisation for propensity fields of the principle of
`interaction by contact', and follows in the philosophy of nature using
the argument of section 8.2 that the mutual interaction of distinct
substances presupposes that they have an extensive relation with respect
to one another. It may be concluded from these two arguments that two
propensity fields may only interact if they overlap in spacetime, and
that, if they do interact to produce an actual event, then, as shown in
11.1, both fields are reduced in spatial extent
at the time of the event. The likelihood for specific interaction events
occurring will again depend on the form or distribution of the measures of
the two propensity fields, and it is plausible that the probability of
interaction will depend on something like the product of the two fields.
Exactly how it works is of course for physics to determine.
The difficulty with this option is that it does not seem to be true of the
quantum world.
There are many instances of interactions between quantum
mechanical substances which do not appear to be definite
outcomes, in the sense of definitely occurring, or definitely not
occurring.
One such kind of interaction is between a low energy neutron and the atoms
in a crystal from which it is being diffracted. The neutron is reflected
from the crystal as though from a mirror or a diffraction grating, but,
although this reflection arises from its interactions with all the atoms,
no single interaction can be said to definitely occur or not occur.
Rather, all the interactions appear to be operating in some conjoint
fashion, as the subsequent propensity field of the neutron does not
radiate out from any single atom, but remains spread out, as if it
interacted with all the atoms together. It did not interact with any
single atom actually and irrevocably.
Another such kind of interaction occurs in an interferometer between the
photons (or neutrons) and the various mirror surfaces. These reflection
interactions cannot be actual, with only one alternative actually
occurring, otherwise interference effects would never be observed.
A third kind of non-actualising interaction occurs when the diffraction
pattern of an electron is deformed as it passes through subsequent
electric or magnetic fields. If we treat electromagnetic fields as
interactions with photons, then these photons are able to interact with
the electron without a specific localisation, by means of
events which are `virtual' rather than actual.
Quantum field theory, the more advanced form of quantum mechanics, has
all potentials arising from the exchange of `virtual
particles'. These would be photons (for electromagnetic potentials),
gluons (for nuclear interactions), W and Z bosons (for weak nuclear
interactions), and presumably gravitons too for gravitational forces. The
potential fields are not now continuously variable, but are composed
of discrete `field quanta' (i.e. virtual particles), and these interact with
ordinary substances via virtual rather than actual events.
It thus appears that propensity fields can interact with each
other, but without producing a fully actual result. These more gentle
interactions are called `virtual events' in quantum physics, and are as it
were the `hidden ingredients' of the many-body wave function
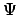 , so that
it includes implicitly the necessary kinds of interaction potentials. If
propensity fields can interact with each other by means of vitual events,
as distinct from actual events, then the propensity that makes up quantum
substances cannot be just for pure actual entities, but must have some
more complicated characterisation. , so that
it includes implicitly the necessary kinds of interaction potentials. If
propensity fields can interact with each other by means of vitual events,
as distinct from actual events, then the propensity that makes up quantum
substances cannot be just for pure actual entities, but must have some
more complicated characterisation.
From the examples above, it does not seem empirically tenable to hold that
all interactions must be actual events, although it may be logically
possible. However much it may be a simple application of our `logic of
process', we are obliged to consider other alternatives.
According to the second option, `virtual events' are already included in
the quantum wave function
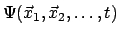 , and actual events are the point localisations of this field.
That is, we take over Schrödinger's equation unchanged, and
supplement by an actualising process which intermittently localises the
dispersed wave field to successive points in space and time. We now want to
examine the consequences of having point localisations. This
assumption was made in chapter
8,
where it was explicitly assumed that actualities were at point places in
our four-dimensional space and time.
This assumption was a `contingent identification' of a term in the process
logic, and is hence not absolutely necessary. In fact, it is almost
certainly wrong, as we shall now see. , and actual events are the point localisations of this field.
That is, we take over Schrödinger's equation unchanged, and
supplement by an actualising process which intermittently localises the
dispersed wave field to successive points in space and time. We now want to
examine the consequences of having point localisations. This
assumption was made in chapter
8,
where it was explicitly assumed that actualities were at point places in
our four-dimensional space and time.
This assumption was a `contingent identification' of a term in the process
logic, and is hence not absolutely necessary. In fact, it is almost
certainly wrong, as we shall now see.
The principal difficulty is that if point localisation did occur, then,
though the propensity field would then (momentarily) have a completely
determinate spatiotemporal form, its momentum (i.e. velocity)
and energy distributions would become completely
indeterminate. This is a simple consequence of the fact that a
point distribution is that of a delta-function, and hence has a Fourier
spectrum with all frequencies without abatement.
This indeterminacy in momentum would perhaps be acceptable if it existed
only momentarily, like the spatiotemporal localisation. But since energy
and momentum are conserved, the momentum and energy distributions will be
unchanged with time. The infinite spread of momentum will thus
persist, and the field will, in `hardly any time at all', spread out over the
entire universe!
This infinite range of momentum and energy is a problem independent of
another fact in ordinary quantum mechanics. There, it is impossible to
localise wave packets to points, as that would require the measuring
apparatus to have particles with infinitely small wavelengths, and hence
infinite energies. This is an independent problem, because the point
localisations being proposed for propensity fields are the characteristic
products of these fields, and do not depend on the point
localisation of any other fields.
If we had to use potentials in Schrödinger's equation, then point
localisation would require an infinite amount of energy prior
to the event, but the spontaneous point actualisation of propensity fields
(as being considered) does not require the input of any energy at all. The
trouble is rather that point actualisation seems to produce an
infinite amount of energy in the fields after the event.
In general, we would wish to see, for any proposed scheme for
actualising, that the effects of the actualisation are a
selection of the field extent not only at the time of the
actualisation, but also at all subsequent times. We could call
this a Principle of Selection, as an expression of the
facts that actualities are a limited form of potentiality, and that
propensity fields are the potentialities for future possibilities over a
wide range of times. The principle is clearly violated by the point
localisations being considered here, as immediately following,
the propensity fields rapidly spread out independently of what
they had been previously.




Next: 11.2 Actual and Virtual
Up: 11. Two Stages of
Previous: 11. Two Stages of
Prof Ian Thompson
2003-02-25
|
![]()